| Definitions |  x:A. B(x), x:A. B(x),  , RandomVariable(p;n), x(s), P , RandomVariable(p;n), x(s), P   Q, {i..j Q, {i..j }, P & Q, t }, P & Q, t  T, T,  , Top, S , Top, S  T, i T, i  j < k, j < k,   x. t(x), if b then t else f fi , tt, ff, x. t(x), if b then t else f fi , tt, ff,  A, t ...$L, rv-partial-sum(n;i.X(i)), rv-const(a), A A, t ...$L, rv-partial-sum(n;i.X(i)), rv-const(a), A  B, False, B, False,  T, True, P T, True, P   Q, P Q, P    Q, r * s, (i = Q, r * s, (i =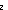 j), r < s, r + s, a < b, a <p b, j), r < s, r + s, a < b, a <p b,  b, a < b, a < b, p b, p   q, x f y, q, x f y,   , t.2, g , t.2, g oset, g oset, g set, set,   , t.1, < , t.1, <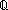 +>, q_le(r;s), p +>, q_le(r;s), p   q, qpositive(r), r - s, i <z j, q, qpositive(r), r - s, i <z j,   b, qeq(r;s), (x.F(x)) o X, r b, qeq(r;s), (x.F(x)) o X, r  s, q*X, X s, q*X, X  Y, a Y, a  b, A c b, A c B, SQType(T), {T}, Outcome, B, SQType(T), {T}, Outcome,  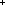 , (X(n) , (X(n)  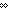 as n as n  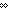 ), ),  x:A. B(x), P x:A. B(x), P  Q, suptype(S; T), a Q, suptype(S; T), a 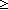 b, b,   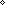 , a , a 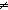 b b  T , (r/s), T , (r/s), 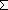 a a  j < b. E(j), j < b. E(j), 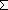 (r) i (r) i  k < j. E(k), < k < j. E(k), <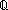 +*>, +*>, 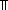 lb lb  i < ub. E(i), r i < ub. E(i), r +gp, +gp,  (op,id) lb (op,id) lb  i < ub. E(i), *, e, +r, 0, Y, 1/r, FinProbSpace, i < ub. E(i), *, e, +r, 0, Y, 1/r, FinProbSpace,  , Unit, Dec(P), SqStable(P), , Unit, Dec(P), SqStable(P),  |
| Lemmas | slln-lemma2, nat wf, int seg wf, rv-disjoint wf, length wf nat, top wf, rationals wf, le wf, random-variable wf, subtype rel function, expectation wf, int inc rationals, rv-compose wf, qmul wf, finite-prob-space wf, rv-partial-sum wf, eq int wf, bool wf, iff transitivity, assert wf, eqtt to assert, assert of eq int, rv-const wf, bnot wf, not wf, eqff to assert, assert of bnot, not functionality wrt iff, rv-scale wf, qdiv wf, int-rational, int-eq-in-rationals, qle wf, squash wf, true wf, p-outcome wf, qsum wf, sum unroll base q, expectation-rv-const, qless wf, qadd wf, qadd preserves qless, qadd comm q, qadd ac 1 q, qinverse q, mon ident q, rv-partial-sum-monotone, q-square-non-neg, bounded-expectation, qless transitivity 1 qorder, decidable int equal, qle weakening eq qorder, rv-le wf, int nzero-rational, nat plus inc int nzero, false wf, nullset-monotone, rv-unbounded wf, qabs wf, q-not-limit-zero-diverges-2, qmul-positive, qmul preserves qle, qless transitivity 2 qorder, qmul comm qrng, qle transitivity qorder, prod sum l q, qsum-non-neg2, qle functionality wrt implies, nat plus wf, sq stable from decidable, decidable qle, qabs-squared, sum split q, qadd preserves qle, qadd inv assoc q, nequal wf, nat plus inc, sum unroll lo q, qadd ident |